摘要：给出了电感耦合并联谐振DC-DC变换器的原理电路，通过分析得出了变换器的稳态特性，利用PSPICE进行了仿真分析。

关键词：电感耦合；变换器；仿真；DC-DC

DC-DC变换器常采用并联谐振形式，即通过储能元件电感与电容的能量交换达到DC-AC-DC的变换任务。从电路结构上来看，一般多采用电容耦合型(PRC-CC)，即其中AC-DC的能量转换是通过谐振电容的耦合取出交变电压，再经整流滤波实现。同样，若通过谐振电感的耦合取出交变电压，经整流滤波实现AC-DC的能量转换，则称为电感耦合型(PRC-IC)。本文给出一电感耦合型并联谐振变换器并采用叠加的分析方法对其进行稳态分析，即将输入方波电压和输出方波电流看作是对谐振回路的2个独立的激励源，然后利用叠加原理进行分析推导，得出了谐振回路的稳态工作特性。利用PSPICE对其进行了分析验证。

1  电路及稳态分析
1．1  电路及波形
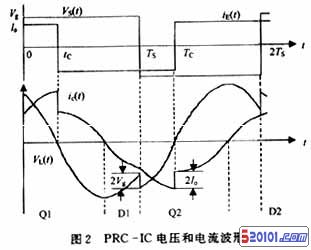
图1(a)是电感耦合并联谐振变换器的原理电路图，图1(b)是其简化电路。图中Q1和Q2是2个开关管，通过他们的交替导通，在电感L和电容C上产生交变电压和电流，其工作波形如图2所示。


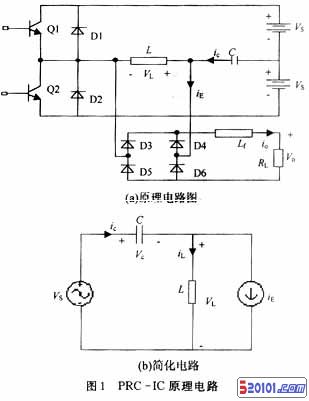
1．2  稳工分析
在对电路进行稳态分析时，将VS(t)和iE(t)分别看成是2个独立的激励源，他们分别对电路作用分析如下。

1．2．1  电压源单独作用
电压源VS(t)单独作用时，假定VS(t)≠0，iE(t)＝0。则根据图1(b)电路写出微分方程：

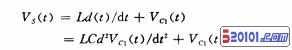
从图2看出，外加方波VS(t)是半波对称的，他的傅里叶级数展开式不包含偶次谐波成份，将这个电压信号代入(1)和(2)两个线性微分方程中，就可得到VC1(t)和iL1(t)两个响应，这2个量也不包含偶次谐波，因此VC1(t)和iL1(t)都是半波对称的，


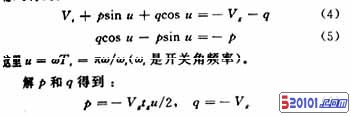
其中是谐振角频率，p和q可用VC1(0)＝-VC1(Ts),dVc1(0)/dt=-dVc1(Ts)/dt从式(1)中确定，可得出：

1．2．2  电流源单独作用
电流源单独作用时，假定iE(t)≠0，VS(t)＝0
电路的微分方程可写为：



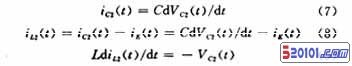
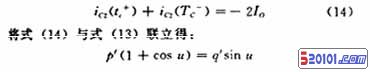
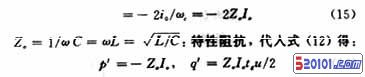
由于iC2(t)是电容中的电流，不是状态变量，即不一定是连续的，所以iC2(tc)＝iC2(TC)不能直接代入式(13)，可根据图2得：


1．2．3  变换器模型
以上分析了图1(b)中VS(t)和iE(t)单独作用的响应，应用叠加原理可得：

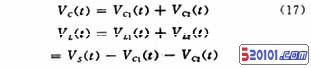
其中VC1(t)和VC2(t)分别对应式(3)和式(11)，从图2和式(18)可得：

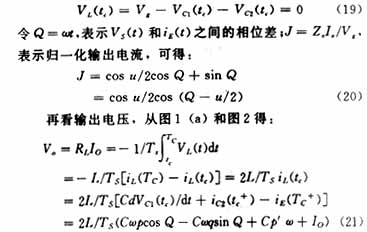
令M＝VO/Vg表示归一化输出电压，将式(6)和式(16)联立可得：

方程(20)和(22)表明可以通过改变参数Q得到某一变量u下的M对J的关系，然后再去
[Page]掉Q可得到：

式(23)表明，M与J之间是椭圆关系曲线。

2  仿真分析
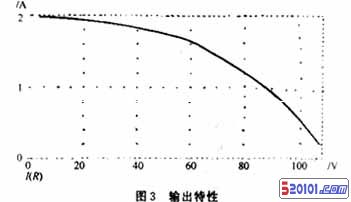
利用PSPICE对其电路进行仿真分析，电路参数取值如下：L＝50μH，C＝6μF，Lf＝2 mH，RL＝75Ω，t＝100μs时的输出特性如图3所示。


3  结语
本文通过将电感耦合并联谐振变换器的输入方波电压和输出方波电流看作是2个相互独立的激励信号对其应用叠加原理来分析计算电路的输出特性，得出工作在连续导电方式下的输出电压和电流特性是一椭圆曲线，这一结论经计算机仿真分析得以证实。