§2.2 颜色的计量系统

　

在2.1节中介绍了颜色的视觉理论，并从定性的角度介绍了颜色的混合规律。在实际工程中往往需要对颜色进行计量和对颜色的混合进行定量计算，CIE为此制定了一整套颜色测量和计算的方法，称为CIE标准色度学系统。其中，它包括好几种不同的计色系统。本节主要介绍物理RGB计色系统和XYZ计色系统。

2.2.1 RGB计色制与麦克斯韦三角形

一、配色试验

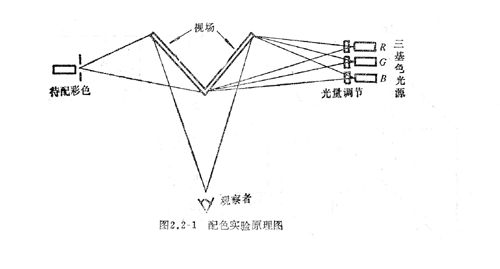
图2.2－1所示的比色计中有两块互成直角的白板（屏幕）将观察者的视场分为两部分，它们对所有可见光谱几乎全反射。将待配色光F投射到屏幕左边，三种基色光投射于屏幕右边，分别调节它们的强度，直到它们的混合光与待色光F的亮度完全一致为止。此时，整个视场将出现待配光的颜色。

二、三基色单位的选定

进行配色试验，必先选定三基色单位；根据不同三基色单位，可分为不同的计色制。在RGB计色制中，国际照明委员会（CIE）规定：把波长为700nm，光通量为1光瓦的红光作为一个红基色单位（或称单位量），用[G]表示；把波长为435.8nm，光通量为0.0601光瓦蓝光作为一个蓝基色单位，用[B]表示。比色计的读数将按基色单位[R]、[G]、[B]进行刻度，而不按辐射功率或者光通量刻度。

红、绿、蓝基色波长的选择，是采用汞弧光谱中经滤波后的单一谱线作为观标准的。它们容易获得，色度稳定而准确，配出彩色也较多。光通量如此确定就是使。

1[R]+1[G]+1[B]=白 （2.2-1）

此时，白的光通量等于5.6508光瓦。

三、配色方程与色系数

选定三基色单位后，就可以进行配色试验。对于任意给定的彩色光F，如果三基色调节装置中的读数分别为R、G、B，就可以写出配色方程

F＝R[R]+G[G]+B[B] （2.2-2）

上式中等式的含义是“可由.......混合配出”，式中R、G、B称为三色系数，它们之间的比例关系决定了所配色光的色度，它们的大小决定了所配色光的光通量：

[F]＝（R＋4.5907G+0.0601B）光瓦

＝（R＋4。5907G+0。0601B）流明 （2.2-3）

在式（2.2－2）和式（2.2－3）中，F是代表具有亮度和色度的彩色光。[F]是代表彩色F的亮度，通常用光通量单位。由式（2.2－1）可推出

r[R]＋r[G]+r[B]= 白 （2.2-4）

因为在式（2.2－1）和式（2.2－4）中，两组三色系数的比例都是1：1：1，所以色度不变，都应配出等能白光E白，只是后者的光通量是前者的r倍。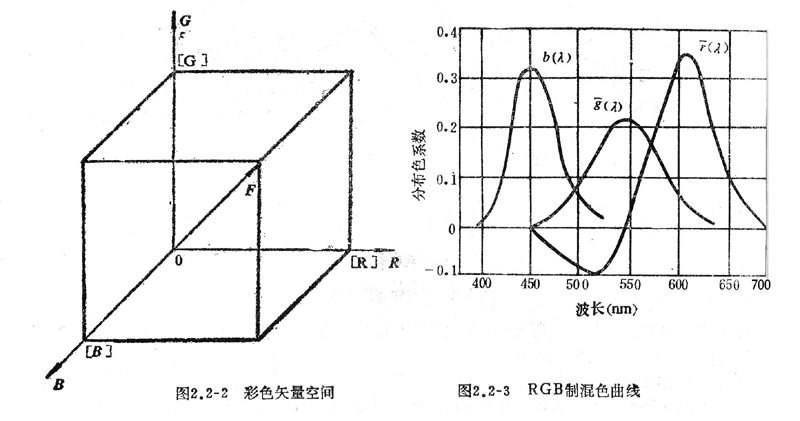

如果用相互垂直的三个坐标轴分别表示三色系数R、G、B，则任意一个彩色F就能用三维空中的一个彩色矢量表征，如图2.2－2所示。

四、分布色系数与混色曲线

利用配色试验所得数据，常因人而异。因此，CIE推荐了一种国际通用的标准分布色系数数据，它是由很多正常视觉观测者的观测结果取平均所组成。所谓分布色系数是指辐射功率为1瓦（注意，不是1光瓦）波长为l 的单色光所需要的三基色的单位数，分别

用，和表示。若用表示辐射功率恒定为1瓦，但波长l 可改变的单色光，则

通过大量实验，CIE分别于1931年和1964年公布了两组分布色系数的标准数据。1931年的数据适用于1° ～4° 视场，1964年公布的数据适用于大于4° 的视场，表2－1列出了1931年CI公布的部分数据。根据表2－1绘制出分布色系数曲线（称为混色曲线），如图2.2－3所示。

从图2.2－3可见，每条曲线都有一段负值。其含义是：是可见光谱范围内，有些纯度很高的物理学三基色直接相加得到，必须将带负号的一个或二个基色搬到待配的半日单色光一边，才能使比色计两边的彩色完全相同。

若已知某彩色的辐射功率谱,求其三色系数时，可不必再进行配色实验，而直接根据CIE提供的分布色系数数据计算求出：

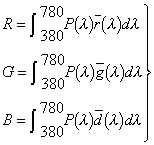
在上式中，若彩色光是等能白光，其功率常数，又所以

上式说明三条混色曲线下的面积是相等的。

五、相对色系数与RGB色度图

在许多情况下，只需要讨论景物与图象的色度，而不涉及其亮度。如前所述，色度只由三色系数R、G、B的比例决定，与它们的数值大小无关。为此，令三色系数之和为[Page]m

并令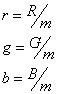

显然上述式中，称为色膜，反映了色光的亮度；r、g、b称为相对色系数或色度坐标，它们的每一组数值都确定了一种颜色的色度。由于相对色系数r、g、b之和等于1。所以知道其中任意二个（例如r和g）就可以算出第三个（例如b=1－r－g）。因此，可以用r－g平面坐标作出包罗所有实际颜色的色度图，即RGB系统色度图。

图2.2－4是RGB色度图，首先确定三基色和标准白光E白的色度坐标，它们的坐标值如表2－2所示。

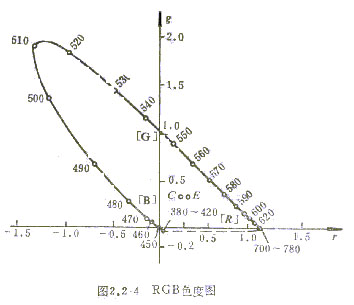
根据谱色光的分布色系数、、,可按下式

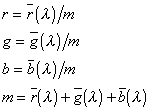（2.2-1）

求出各谱色光的色度坐标值，如表2－1所示。在色度图中，谱色光的轨迹是一条舌形曲线，称为谱色轨迹。

　

g

g

b

红基色

1

0

 0

绿基色

0

1

 0

蓝基色

0

0

 1

等能E白

1/3

1/3

 1/3

[R]、[B]之连线所示的色光是由红基色和蓝基色合成的，中点为品红色，而谱色光380nm和780nm两点坐标之连线所示色光是紫色与红色合成的，中点为紫红色，不过这两条直线几乎是一条直线，颜色也较相近。[R]、[B]连线上的颜色是非常谱色，它和舌形曲线组成一个封闭的马蹄形区域。自然界的一功颜色都在该区域内，称为实际颜色；在该区域外没有实际颜色，称为虚色。

彩色光的色度坐标越靠近谱色轨迹，其饱和度愈高；而愈靠近E白，其饱和度愈低。

六、麦克斯韦计色三角形

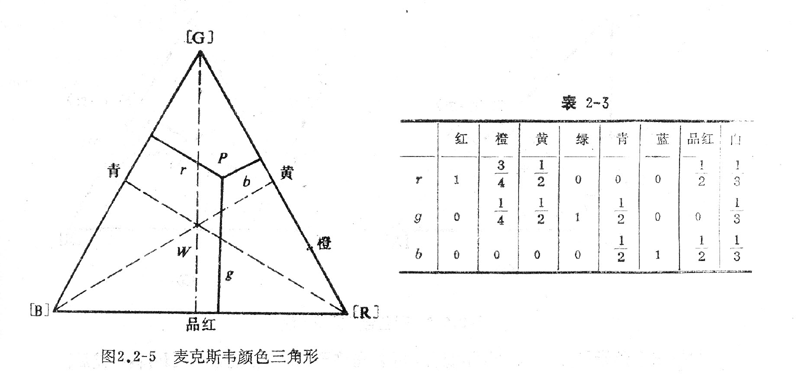
麦克斯韦（J.C.Maxwall）首先用等边三角形简单而直观地表示颜色的色度，这个三角形称为Maxwell颜色三角形，如图2.2－5所示。它的三个顶点分别表示[R]、[G]、[B]，三角形内任一点都代表自然界的一种颜色，如果设每个顶点到对边的距离为1，则三角形内任一点P到三边距离之和等于1（这由几何知识不难证明）。如果令P点到红、绿、蓝三顶点对应的三边的距离分别为r、g、b，则r、g、b就是P点所代表彩色的色度坐标，表2－3列出了红、橙、黄、绿、青、蓝、品红、E白的色度坐标值，由这些色度坐标值就可以确定它们在麦克斯韦颜色三角形中的位置，如图2.2－5所示。

七、彩色的合成

通过大量配色试验证明：合成彩色的三系数分别等于各混合彩色对应色系数之和。根据上述规律，可以不必进行配色试验，而通过“计算法”或“图解法”求出合成彩色。

1、计算法

已知：两个彩色光和的配色方程分别为

求：，相混后的合成光依上述彩色光的相加规律有

（2.2-12a）

或者

（2.2-12b）

除计算法外，还可以在r－g直角坐标式或麦克斯韦三角形中，用图解法求合成光的色度坐标；这种方法完全类似于力学中求两质点重心的位置。详述如下：

将（2.2－式2b）改写成

（2）

上式中

（2.2-14）

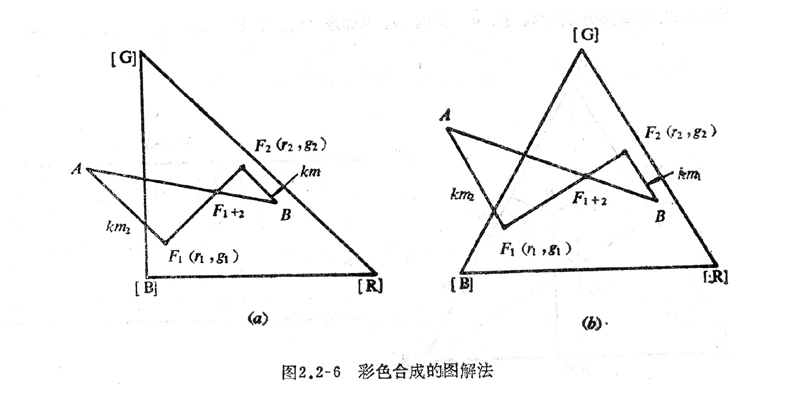
上式中所示列三个公式与力学求重心的公式相类似，因此，可采用求重心的方法，求解合成光的色度坐标。在图2.2－6所示的r－g直角坐标系或麦克斯韦颜色三角形，先找到和的坐标点，在和连线上反向地垂直引出两段长度为和的线段和，其中r可为任意常数，直线和相交于C点，C点是合成光的坐标。由此可见，和两色光按不同比例混合时，合成光总是在直线上。

如果三个色光、、相混合，可以先将和相混合得到然后再将和相混合，得到合成光。不论三个色光按什么比例得混合，混合色光必然处在D 之内。换句话说，利用三个基色只能混合得到以基色为顶点的三角形以内的各种颜色。彩色电视中，应使彩色显像管三基色组成的三角形面积尽可能的大，这样才能使重现的彩色更加丰富多彩。

2.2.2 XYZ计色制与CIE色度图

RGB计色制的基础是配色试验，它的物理意义明确，但使用不方便。因为，必须知道彩色光的三个色系数R、G、B，才能处出其亮度； 分布色系数中存在负值，用求和法近似计算色系数时，容易出错；自然界某些实色的相对色系数出现负值，它们的坐标不全在第一象限，作图不方便，为了克服上述缺点，1931年CIE在RGB计色制的基础上采用三个虚设的颜色作为计算三基色单位，分别用[X]、[Y]、[Page][Z]表示，从而建立了XYZ计色制，并绘制了新的色度图－－CIE色度图。

XYZ计色制不能象RGB计色制那样，一切计算结果都可以通过配色试验来验证，它是在RGB制的基础上通过数学运算转换产生的一种计色制。在学习XYZ制时，要注意与RGB制进行对比，抓住它们的异同点以及相互转换关系。

一、基色单位的选定

设XYZ的三基色单位是[X]、[Y]、[Z]，则任一彩色的配色方程为

F＝X[X]＋Y[Y]＋Z[Z] （2.2-15）

式中，X、Y、Z称为三色系数，三基色单位的选定基于如下考虑：

1、要求自然界所有实色的三个色系数X、Y、Z为非负数，以利于色度计算与作图。

2、为了简化彩色的亮度计算，规定彩色的亮度直接由色系数Y决定，且1[Y]的光通量是1光瓦，而与另外两个色系数X、Z无关。彩色的色度仍由X、Y、Z的比值决定。

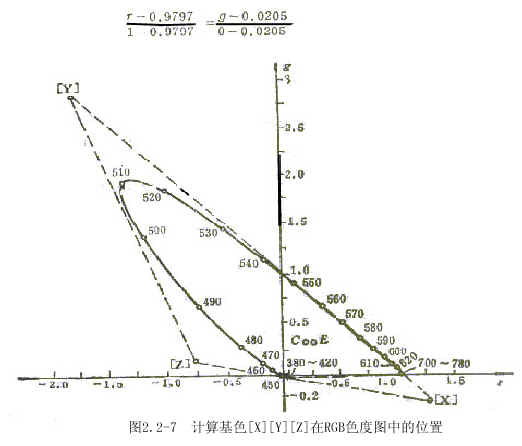
3、当X＝Y＝Z，仍代表等能白光E白。

根据以上三点要求，就可以找出三基色单位[X]、[Y]、[Z]在r－g色度坐标中的位置，从而确定了[X]、[Y]、[Z]与[R]、[G]、[B]之间的相互转换关系。

按第一个要求，所有实色的X、Y、Z应为非负数，故以[X]、[Y]、[Z]为顶点的三角形，必须包围图2.2-7中的马蹄形区域，否则X、Y、Z将出现负数。在RGB色度图中，由于540nm到700nm谱色轨迹近似为一直线，将其延长作为颜色三角形的[X]、[Y]边。已知700nm和640nm的色度坐标分别为g ＝1，g＝0和g ＝0.9797，g＝0.0205可写出两点式直线方程是

整理得直线[X][Y]的方程为

g ＋0.99g－1＝0 （2.2-16）

由于510nm至380nm之间的谱色轨迹为一曲线，CIE规定取一条与光谱轨迹上503nm点相靠近的直线作为[Y][Z]边，这条直线的方程是

1.45g ＋0.55g＋1＝0 （2.2-17）

根据第二个要求，单位基色[X]和[Z]的光通量应为零，X[X]和Z[Z]的合成光的光通量也应为零，所以[X]、[Z]的连线是一条光通量等于零的直线，该直线的方程是

g ＋4.5907g＋0.0601b＝0

因为g ＋g＋b＝1，所以上式可变成：

0.9399g ＋4.5306g＋0.0601＝0 （2.2-18）

上式就是零光通量直线[X][Z]的方程。

对以上三个直线方程式（2.2-16）、式（2.2-17）和式（2.2-18）两两联立求解，可得到它们的交点[X]、[Y]、[Z]在g －g坐标系中的色度坐标值：

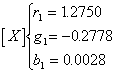
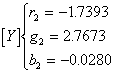
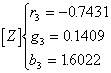
（2.2-19）

若令

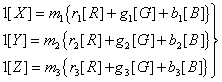（2.2-20）

根据第二条规定，1[Y]的光通量等于1光瓦，所以

（2.2-21）

将式（2.2-19）中[Y]的坐标值代入上式得 ＝0.0912

根据第三条规定，当X＝Y＝Z时，仍代表等能白光E白，所以1[X]＋1[Y]＋1[Z]也应代表1光瓦的E白。由式（2.2-20）可得：

1[X]＋1[Y]＋1[Z]＝

（2.2-22）

由式（2.2-4）可知，只有[R]、[G]、[B]前面三个色系数相等时，才能代表E白，所以可得下列两个独立的方程

（2.2-23）

将和式（2.2-19代入式，得）

（2.2-24）

把m值和式（2.2-19）代入式（2.2-20）得到由物理三基色单位[R]、[G]、[B]求计算三基色单位[X]、[Y]、[Z]的转换关系式：

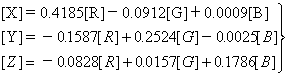（2.2-25）

若用矩阵形式表示，则

=[A] （2.2-26a）

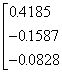
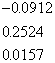
[A]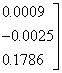＝ （2.2-26b）

若逆矩阵运算可知

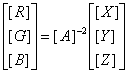（2.2-27a）

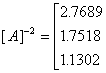
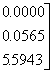（2.2-27B）

二、配色方程与色系数

XYZ制的配色方程已由式（2.2-15）给出，任一彩色可用

F＝X[X]＋Y[Y]＋Z[Z]

表示，X、Y、Z称为三色系数。对同一彩色，也可以用RGB制的配色方程

F＝R[R]＋G[G]＋B[B]

表示。对于同一彩色，以上两式右边应相等：

R[R]＋G[G]＋B[B]＝X[X]＋Y[Y]＋Z[Z]

将式（2.2-25）代入上式右边得

R[R]＋G[G]＋B[B]＝（0.4185X－0.1587Y－0.0828Z）[R]

＋（－0.0912X＋0.2524Y＋0.0157Z）[G]

＋（0.0009X－0.0025Y＋0.1786Z）[B]

上式两边对应系数应相等，所以

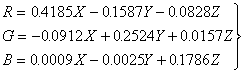（2.2-28）

上式改用矩阵表示

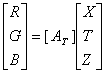（2.2-29）

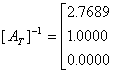
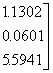（2.2-30b）

从式（2.2-26b）和式（2.2-29b）、式（2.2-27b）和式（2.2-30b）可以看出：矩阵[A]和、和都互为转置矩阵；而[A]与，和都互为逆矩阵。所以在上述四个矩阵中，知其一，可求其三。

三、分布色系数与混色曲线

[Page]

与RGB计色制相似，XYZ计色制的分布色系数也是指配出辐射功率为1瓦的谱色光所需要的[X]，[Y]，[Z]的数量，并分别用，，表示。它们不能用配色试验得出，而是由经计算得到的。

由于式（2.2-29）和式（2.2-30）适用于求任意彩色的色系数，分布色系数是色系数中的一种特殊情况，因此

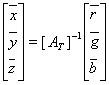（2.2-31）

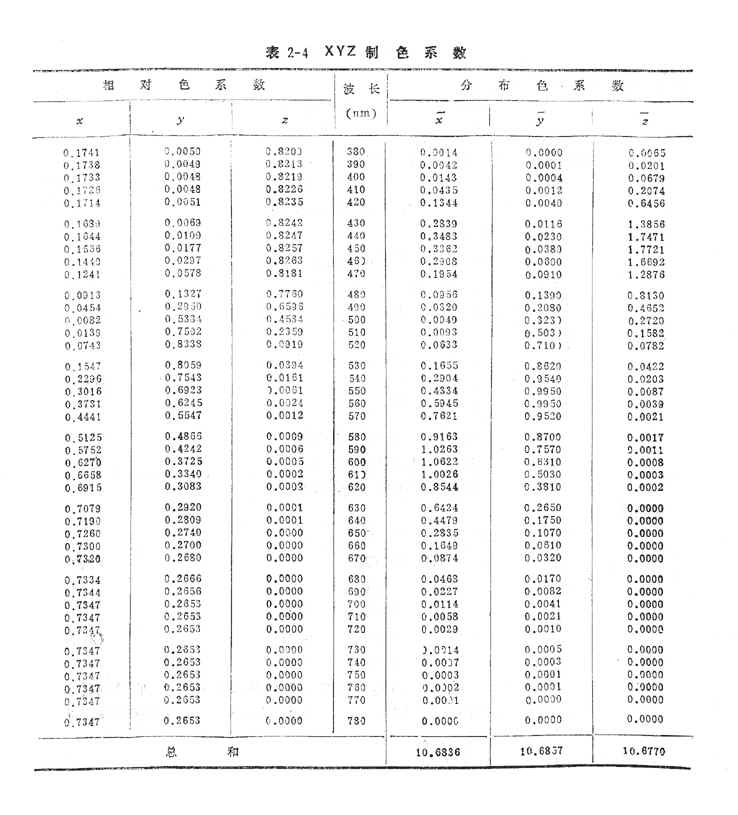
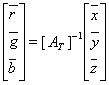（2.2-32）

　

以上两式中和的数据见式（2.2-29b）和式（2.2-30b）。根据表2-1的数据，可求出，，的数据和曲线（混色曲线），分别如表2－4和图2.2-8所示。从中可以看出：，，均为非负数，满足制定XYZ计色数的第一条规定； 曲线和相对视敏函数V（l ）曲线一致，这说明彩色的亮度仅由色系数Y决定，这与制定XYZ计色制的第二条规定相一致。

与RGB制类似，若已知某彩色光的功率谱为P（l ），则其三个色系数

，

（2.2-33）

对于等能白光E白，P（l ）＝常数，又X＝Y＝Z，故三条曲线下的面积相等。

四、相对色系数与CIE色度图

与RGB制相类似，彩色的色度也只取决于X、Y、Z的比值，故引入相对系数（或色度坐标）x、y、z和色模m'，它们分别为

（2.2-34）

显然，x＋y＋z＝1 （2.2-35）

此时，配色方程可写成

F＝X[X]＋Y[Y]＋Z[Z]＝ （2.2-36）

相对色系数与分布色系数的关系仍然是

（2.2-37）

上式中，利用上式可求出各谱色光的色度坐标值如表2-4所示。

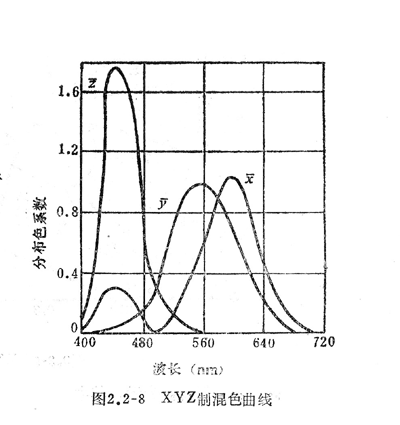
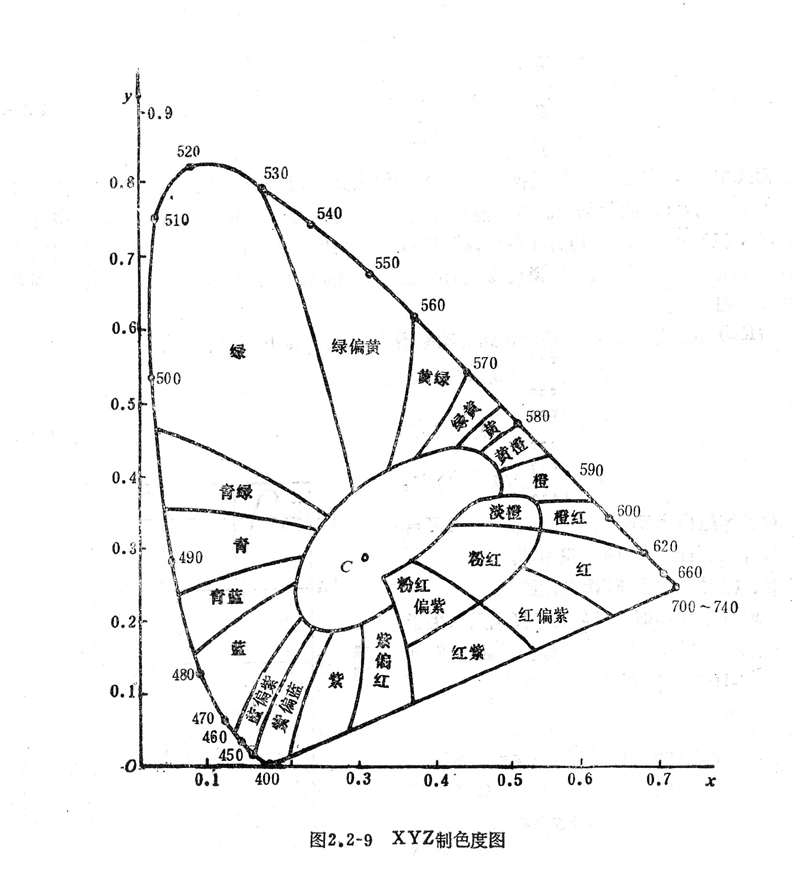
与RGB计色制相类似，可将自然界所有颜色表示在xy直角坐标系中，这就是国际上通用的CIE色度图，如图2.2-9所示。它的用途极广，是色度学中有用的工具。对于任意功率谱的彩色，其色度坐标可用式（2.2-33）和式（2.2-34）求出；或者先求它们的RGB制的色系数R、G、B，然后再利用坐标变换成X、Y、Z或x、y、z。

五、彩色的合成

与RGB制相仿，可用计算法或图解法求解彩色合成的问题。

与RGB制不同，XYZ制常用F（x，y，Y）来表示某一彩色，其中x，y表示色度坐标，Y代表亮度。

1、计算法：若已知两个色光为和则合成彩色可用

表示，其中

（2.2-38）

上式中，。

2、图解法：合成光位于两个混合色光、的连线上，它到和两点的距离之比等于，具体作图求解方法与RGB制完全相同，此处不再赘述。

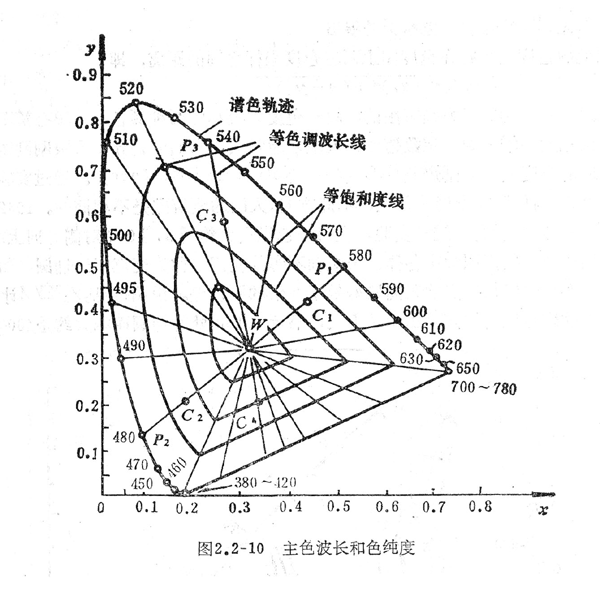
六、主色波长和色纯度

颜色的色度可直接用反映色调的主色波长与色纯度（即饱和度）来表示。

1、主色波长与补色波长

在图2.2-10中设位置是W点，对于任意彩色，射线W与谱色轨迹相交于点，点的谱色波长为，称为彩色的主色波长；的反延长线与谱色轨迹相交于点，点对应的谱色波长，称为彩色的补色波长。对于位于线段上的彩色，它的主色波长是，而补色波长为。由于D RWB（R点和B点分别指谱色轨迹上780nm和380nm两点）内和线段上的彩色均为非谱色，故彩色无主色波长，只有用它的补色波长（即彩色的主色波长），间接表示它的色调。

2、等色调波长线和等饱和度线

在线段上各点的色调都与波长为的色调相同，只是色纯度各异。越靠近谱色轨迹，色纯度越高；愈靠近白光W点，色纯度愈低；白光W的饱和度等于零。称为等调波长线（或主色波长线），同样，线段，，…都称为等色调波长线。任一彩色的色纯度

（2.2-39a ）

（2.2-39b）

上式中，和分别为白光W，彩色C和谱色P三点的色度坐标。当等色调波长线近乎平行x轴时，只能用式（2.2-39a），当它近乎平等y轴时，只能用式（2.2-39b）。在非上述情况下，两式均可任意选用。

由波长不同但色饱和度相同的各点连成的曲线称为等饱和度线。若彩色的主色（或补色）波长和饱和度已知，则其色度被确定。应注意：彩色的主色波长和饱和度，随基准白光的不同而各异。例如某点色度坐标为x＝0.2000，y＝0.650。若选E白作基准白光，＝526.7nm，＝0.651；而选C白作基准白光时，＝529.1nm，＝0.671。某一颜色的色调和色饱和度跟它的色坐标之间的关系，类似解析几何中极坐标与直角坐标的关系。

七、色域图

各种颜色在色度图上的位置，可用图2.2-9所示的色域图表示，该图分成许多小区，每一小区代表一种颜色。[Page]

各种颜色的色度，无论是用色度坐标或用主色波长和色纯度来表示，均需两个参量，方能确定。但对于谱色轨迹上的谱色光，因其色饱和度最高都等于1，所以只需知其波长就能确定它的色度坐标。

2.2.3 均匀色标制

一、刚辨差（JND）与均匀色标制的提出

两种颜色的色度差是指在色度图上两者色度坐标之间的距离，即

（2.2-40）

　

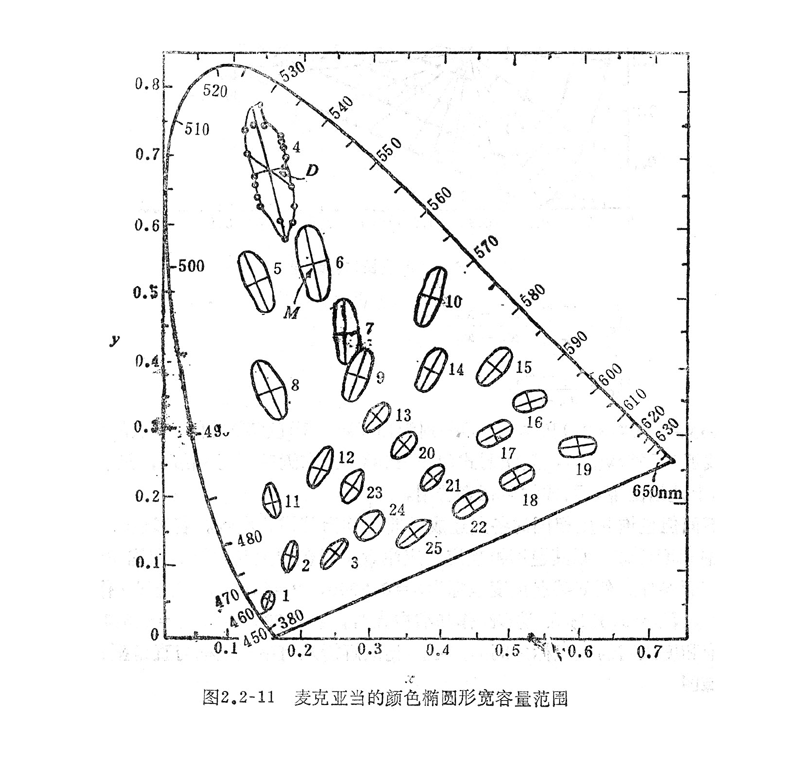
由人眼分辨颜色变化的能力是有限的，故对色度差很小的两种颜色，人眼分辨不出它们的差异。只有当色度差增大到一定数值时，人眼才能觉察出它们的差异，人眼刚刚能觉察出颜色差别所对应的色度差称为刚辨差JND（Just Noticable Diference）。通过实验表明：在CIE色度图上，不同位置或者同一位置的不同方向，人眼的刚辨差是不相同的。1942年麦克亚当（Macadam）对25种色光进行实验，在每个色光点大约沿5到9个对侧方向上测量刚辨差。结果得到的是一些面积大小各异、长短轴不等的椭圆，称为麦克亚当椭圆，如图2.2-11中，不同位置的麦克亚当椭圆面积相差很大，靠近520nm处的椭圆面积大约是400nm处随圆面积的20倍。这表明人眼对蓝色区域颜色变化相当敏感，而对饱和度较高的黄、绿、青部分的颜色变化不太敏感。对于面积大小相同的区间，在蓝色部分比绿色部分，人眼能分辨出更多的颜色。在XYZ计色坐标系中，刚辨差的不均匀性给颜色的计量与复现工作造成麻烦。人们曾经作过试探，将CIE－XYZ色坐标系经过一定的线性变换（或投影变换），企图使整个色域内各点的刚辨差相等，麦克亚当椭圆都变成半径相等的圆。试探结果表明，上述设想是无法实现的。但是经过某种投影变换，能使各点的刚辨差的均匀性比XYZ计色坐标系要好得多，这就是均匀色标系统（制）。

二、均匀色标制

均匀色标系统又称为UCS（Uniform Chromaticity Scale）制，1960年它被CIE正式承认采用。在UCS制中，规定均匀色度坐标的横坐标为u，纵坐标为v，而u和v都是从x和y值的线性变换得来的，其相互关系是：

（2.2-41a）

（2.2-41b）

根据式（2.2-41a）将CIE色度图变成用m －坐标表示的色度图，如图2.2-12所示。因为是线性关系，所以CIE色度图中的直线变换到m －坐标中仍是直线。由图可见，原来25种色光的麦克亚当椭圆向圆的方向靠近，各圆的大小差别也变小了。从而使得人眼在视觉上差别相等的颜色，在m －坐标上大致是等距的，这有利于人们根据不同颜色的色度差来判断两者颜色的差别，对颜色计量与重现工作带来方便，特别是，用来作为制定产品颜色公差的依据。通常规定刚辨差的量值单位为JND，在UCS制中，1JND＝0.00384UCS坐标线段值。设两色坐标的设计值、。实际测量值为、。则设计误差为



本小章节完结....请继续浏览下篇